Programmers: 학교 가는 길
Conditions
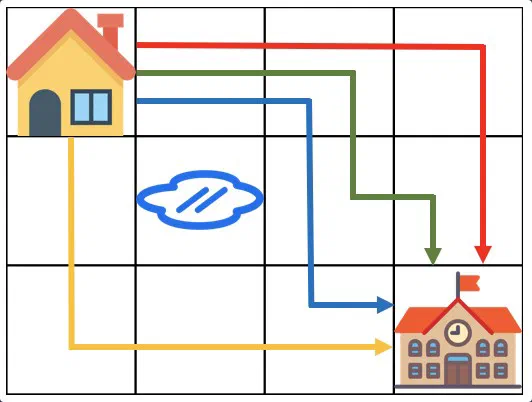
- 집에서 학교까지 가는 길은 $$m \times n$$ 크기의 격자 모양으로 나타낼 수 있음.
- $$m$$, $$n$$은 1 이상 100 이하인 자연수. $$m$$, $$n$$이 모두 1인 경우는 입력으로 주어지지 않음.
- 집의 좌표는 $$(1, 1)$$, 학교의 좌표는 $$(m, n)$$.
- 물에 잠긴 지역인 puddles의 좌표는 0개 이상 10개 이하.
- 집과 학교가 물에 잠긴 경우는 입력으로 주어지지 않음.
- 오른쪽과 아래쪽으로만 움직여 집에서 학교까지 갈 수 있는 최단경로의 개수를 1,000,000,007로 나눈 나머지를 반환.
Design
$$ matrix = \begin{bmatrix} 0 & 0 & 0 & 0 & 0 \ 0 & 1 & 1 & 1 & 1 \ 0 & 1 & -\infty & 1 & 2 \ 0 & 1 & 1 & 2 & 4 \ \end{bmatrix} $$
- 해당 지점까지 올 수 있는 경로의 개수를 이차원 배열로 나타냄.
- $$ m_{ij} $$가 puddle이면 그 지점은 갈 수 없음.
- $$ m*{(i-1)j} $$이 puddle이면 $$ m*{ij} = m_{i(j-1)} $$, vice versa.
- 둘 다 puddle이 아니라면 $$ m*{ij} = m*{(i-1)j} + m_{i(j-1)} $$.
Recursive equation
$$ C[i,j]:\text{ The number of paths from } (1,1) \text{ to } (m,n)\ C[i,j] = \begin{cases} 1, & \text{if } m \text{ = 1 and } n \text{ = 1} \ -\infty, & \text{if } matrix_{ij} \text{ is a puddle} \ matrix_{(i-1)j}, & \text{if } matrix_{i(j-1)} \text{ is a puddle} \ matrix_{i(j-1)}, & \text{if } matrix_{(i-1)j} \text{ is a puddle} \ matrix_{(i-1)j} + matrix_{i(j-1)}, & \text{otherwise} \end{cases} $$
Implementation
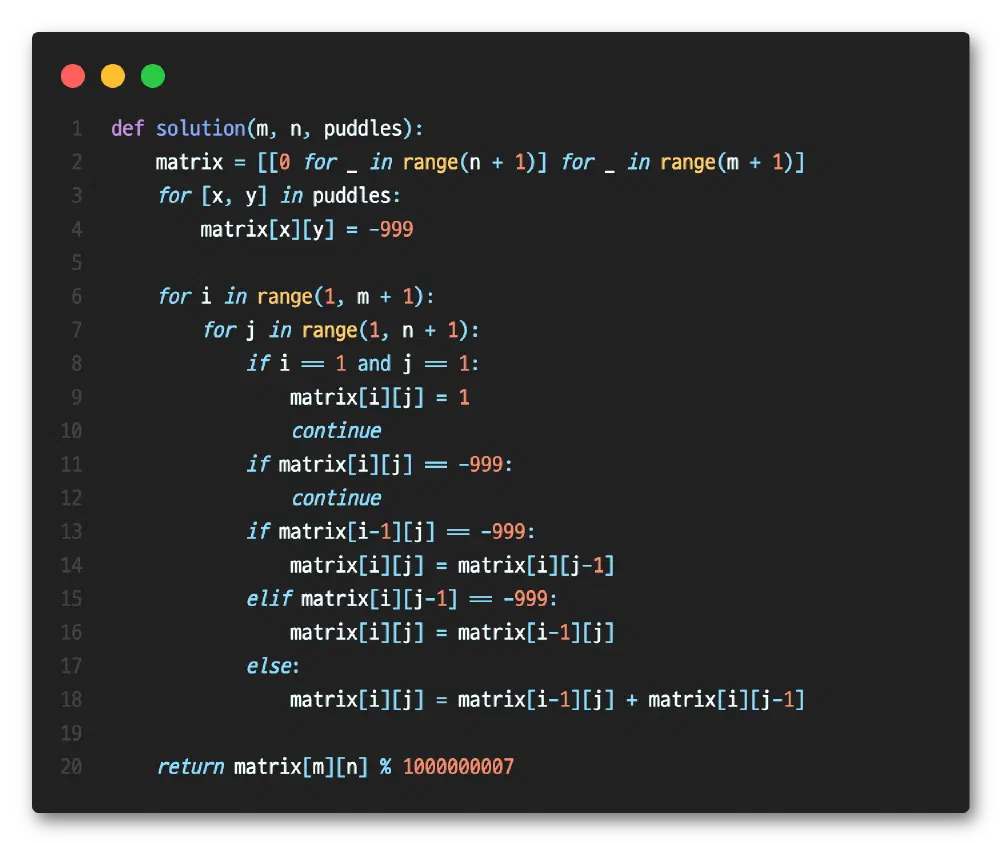
Comments