Programmers: Integer Triangle
Conditions
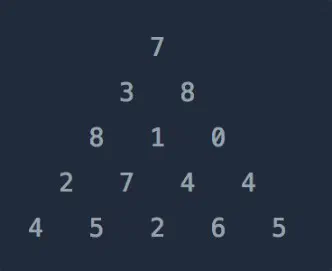
- 위와 같은 삼각형의 꼭대기에서 바닥까지 이어지는 경로 중, 거쳐간 숫자의 합이 가장 큰 경우를 찾음.
- 아래 칸으로 이동할 때는 대각선으로 한 칸 오른쪽 또는 왼쪽으로만 이동 가능.
- 삼각형의 높이는 1 이상 500 이하.
- 삼각형을 이루는 숫자는 0 이상 9,999 이하 정수.
Design
- 이차원 배열 형태로 변경.
$$ \begin{bmatrix} -\infty & -\infty & -\infty & -\infty & -\infty & -\infty \ -\infty & 7 & -\infty & -\infty & -\infty & -\infty \ -\infty & 3 & 8 & -\infty & -\infty & -\infty \ -\infty & 8 & 1 & 0 & -\infty & -\infty \ -\infty & 2 & 7 & 4 & 4 & -\infty \ -\infty & 4 & 5 & 2 & 6 & 5 \end{bmatrix} $$
- $$ m*{ij} $$까지 경로의 최대값은 $$ L*{(i-1)(j-1)} $$ 혹은 $$ L_{(i-1)j} $$ 중 큰 값 + 자기 값.
Recursive equation
$$ L_{ij}:\text{ Maximum length from } (1,1) \text{ to } (i,j)\ L_{ij} = \begin{cases} m_{ij}, & \text{if } i \text{ = 1 and } j \text{ = 1} \ max(L_{(i-1)(j-1)}, L_{(i-1)(j)}) + m_{ij}, & \text{otherwise} \end{cases} $$
Implementation
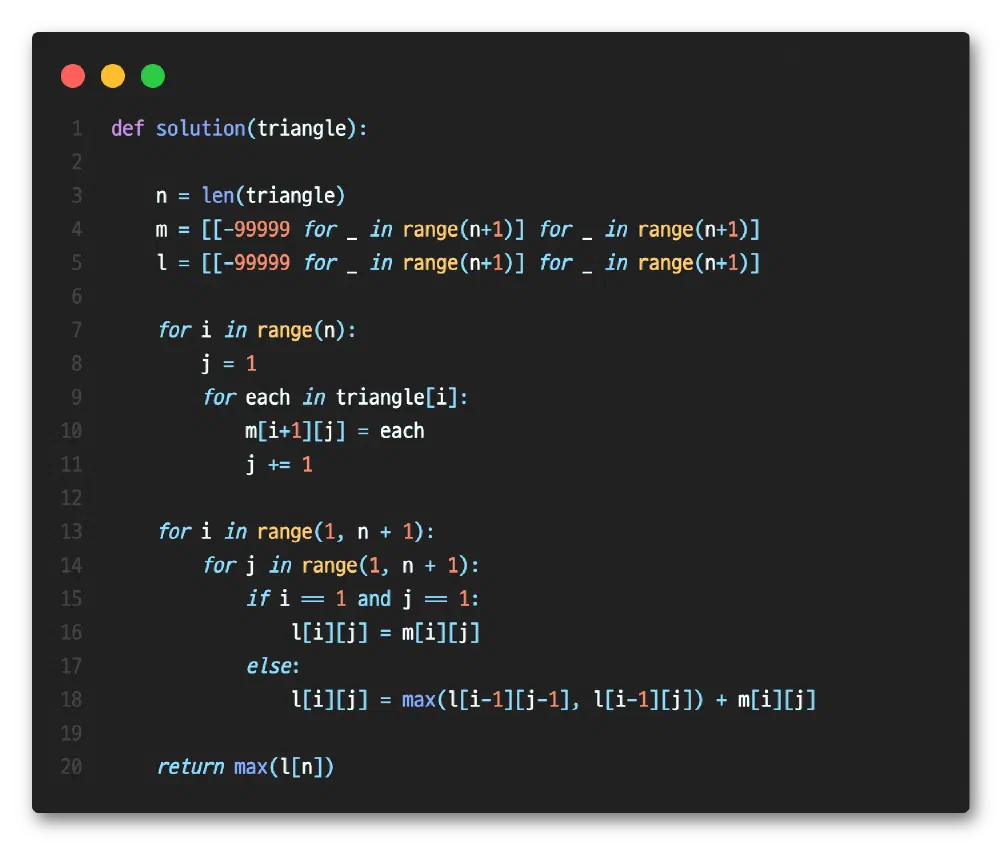
Comments