백준 17070 파이프 옮기기 1

https://www.acmicpc.net/problem/17070

문제 이해

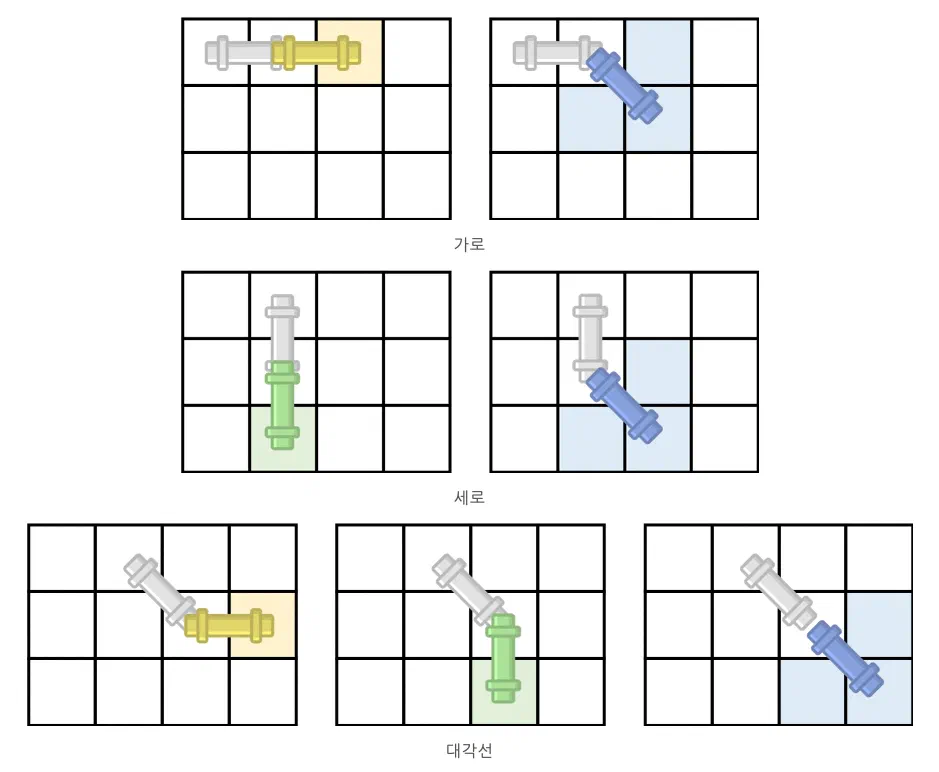
• 집 배열은 (1, 1) 부터 (N, N) 까지인 정사각형 이차원 배열입니다.
• 파이프의 초기 위치는 (1, 1), (1, 2) 입니다.
• 파이프는 반드시 밀어서 이동해야 하고 45도만 회전 가능합니다. 즉, (1, 1), (1, 2)에서 (1, 2), (2, 2)로 옮길 수 없습니다. 그러므로 현재 방향이 가로라면 다음 가능한 진행 방향은 가로 (1, 2), (1, 3) 또는 대각선 (1, 2), (2, 3) 입니다.

접근 방법

• 파이프는 왼쪽이나 위쪽으로 이동할 수 없으므로 파이프의 오른쪽 끝(1, 2)을 기준으로 움직입니다.
  • 이후 지칭하는 파이프는 편의상 파이프의 오른쪽 끝을 말합니다.
  • 그리고 이 조건에 의해 집 배열의 1열은 확인할 필요가 없습니다. (파이프가 왼쪽으로 돌아가지 못하므로.)
• 대각선인 경우 단순히 현재 위치 (i, j)와 파이프 왼쪽 끝 칸 (i - 1, j - 1)만 빈칸이 아니고, (i - 1, j), (i, j - 1)칸도 빈 칸이어야 함을 확인해야 합니다.
• 현재 칸에 올 수 있는 방법의 수를 dp라는 이름의 배열로 관리합니다. 더해서, 이 문제에서는 방향 별로 갈 수 있는 방법이 정해져 있기 때문에 현재 칸에 올 수 있는 방법도 방향별로 카운트 해줍니다.
  • dp를 3차원 배열로 선언합니다. dp[x][y][d]에서 x, y는 2차원 집 배열의 행, 열 좌표를 나타내고, d는 방향(0: 가로, 1: 대각선, 2: 세로)을 나타냅니다.
• 2차원 집 배열을 반복문으로 탐색하며 벽인 곳은 건너뛰고 벽이 아닌 곳에 올 수 있는 방법의 수를 구합니다.
  • (i, j)에 가로 방향으로 올 수 있는 경우는 dp[i][j][0]는 (i, j - 1) 칸이 가로 또는 대각선인 경우입니다. dp[i][j][0] = dp[i][j - 1][0] + dp[i][j - 1][1]
  • 세로 방향으로 올 수 있는 경우도 인덱스만 바꿔서 적용해주면 됩니다.
  • 대각선인 경우가 조금 다른데, 이 때는 (i - 1, j - 1) 칸이 가로, 세로, 대각선인 경우 모두 가능합니다. 대신, (i - 1, j), (i, j - 1) 칸도 빈 칸(벽이 아님)인 경우에만 이동이 가능하므로 조건문을 추가해 줍니다.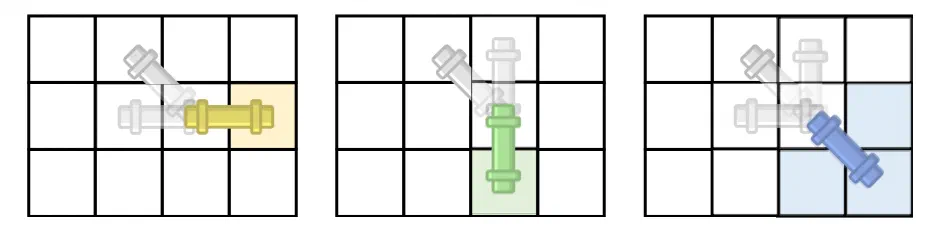
• 마지막으로 어떤 방향으로든 (N, N) 칸에 도착할 수 있는 방법의 수가 실행 결과이므로 각 방향으로 (N, N)에 올 수 있는 방법의 수를 모두 더해 출력합니다. dp[N][N][0] + dp[N][N][1] + dp[N][N][2]

코드

public class Main {

  public static void main(String[] args) throws IOException {
    BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

    // 문제 입력
    int N = Integer.parseInt(br.readLine());
    int[][] map = new int[N + 1][N + 1];

    for (int i = 1; i <= N; i++) {
      StringTokenizer st = new StringTokenizer(br.readLine());
      for (int j = 1; j <= N; j++) {
        map[i][j] = Integer.parseInt(st.nextToken());
      }
    }

    // dp 배열 초기화
    int[][][] dp = new int[N + 1][N + 1][3];

    // 처음 위치: x, y, 방향(0 가로, 1 대각선, 2 세로)
    // 처음 위치를 벽으로 취급.
    dp[1][2][0] = map[1][2] = 1;

    for (int i = 1; i <= N; i++) {
      // 파이프를 오른쪽으로 돌릴 방법이 없으므로 1열은 체크 안해도 됨
      for (int j = 2; j <= N; j++) {
        // 처음 위치(이미 값 할당함) 또는 벽인 경우
        if (map[i][j] == 1) continue;

        // 가로 방향으로 이 칸 올 수 있는 경우는 이전 칸이 가로거나 대각선인 경우
        dp[i][j][0] = dp[i][j - 1][0] + dp[i][j - 1][1];

        // 대각선으로 이 칸에 올 수 있는 경우는 이전 칸이 가로, 대각선, 세로. 빈칸 체크 필요
        if (map[i - 1][j] != 1 && map[i][j - 1] != 1) {
          dp[i][j][1] = dp[i - 1][j - 1][0] + dp[i - 1][j - 1][1] + dp[i - 1][j - 1][2];
        }

        // 세로 방향은 이전 칸이 세로거나 대각선인 경우
        dp[i][j][2] = dp[i - 1][j][1] + dp[i - 1][j][2];
      }
    }
    System.out.println(dp[N][N][0] + dp[N][N][1] + dp[N][N][2]);
  }
}

마무리

이전에 이 문제와 비슷한 백준 5569 출근 경로를 풀어본 경험이 있어 초기 구상이 비교적 수월했습니다. 출근 경로 문제를 풀 때는 이런 유형이 처음이어서 블로그를 참고했는데, 블로그에서는 방향을 포함해 문제를 풀기 위해서 4차원 배열을 사용했습니다.

추가로, 이 문제는 백준 17069 파이프 옮기기 2 문제와 시리즈입니다. 2번의 경우 문제 자체는 동일하나 입력 사이즈만 두 배 (맵 크기는 네 배) 증가한 문제입니다. 소스 코드는 위 코드를 거의 동일하게 사용 가능하나, 입력이 커진 만큼 추가적으로 고려할 부분이 생깁니다.

Prerequisites: 이 글에서 언급되었으나 깊게 설명하지 않은 내용입니다.

• DP (Dynamic Programming, 동적 계획법)